Yes, there is a Third Way. And that is based on passive filter design. The sins of passive speaker-level crossovers are many; after all, these networks are dealing with highly reactive loads at high currents. Not so a line-level crossover, which will have a nice resistive load of the designer’s choice, and is working in the micro-amp regime.
As mentioned before, I am not going to sweat the low-pass filter: at 100Hz and lower, contrary to much audiophile legend, the electronics just aren’t that critical, and one of the commercial jobs with variable phase and perhaps EQ will do nicely. If you want to be totally studly, you can use one of the many excellent digital crossovers like the Behringer DCX. Where 99% of the music sits is the higher frequencies, and it is there that we need to pay special attention; though many are certainly happy with filters like the Behringer, some of us would prefer to have an all-analog signal chain, preferably with the signal avoiding being sliced, diced, re-assembled, and run through silicon.
It’s easy to achieve a first order (6dB/octave) high-pass filter via normal RC coupling, neatly sidestepping the issue. But that slope will not get us to the desired 4th order target (though in systems requiring a third-order 18dB/octave acoustic rolloff, this will be sufficient). We need a second order filter.
The equivalent passive solution for a second order filter is a CLR circuit, similar to the circuits one finds in speaker-level crossovers:
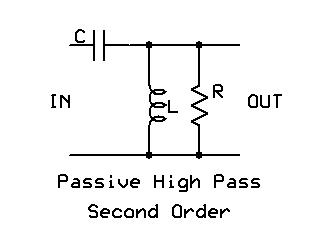
The basic formulas are as follows:
fo = 1/(2pi*sqrt(LC))
Q = (1/R)*sqrt(L/C)
Let’s run through the exercise of calculating values assuming a very low source impedance and a 100k load impedance (typical of tube circuits). That fixes the value of R.
For my particular setup (see here), the required turnover frequency is 110Hz with a Q of 0.707 (Butterworth). Running the numbers, this calls for C to be about 0.01uF (10nF) and L to be slightly over 200H. The capacitor is no problem- it’s a standard value, small, and can inexpensively be a high quality component. The inductor is more of an issue- 200H isn’t an impossibly high value, but it IS a high one, which will call for fine windings and high-quality cores. It will not be cheap (about $150/pair), it will be highly magnetic, and much attention to stray capacitances will make this a pretty critical component. And it will NOT be small, either.
Being large, coiled, and in a high impedance spot, the inductor will also be very effective as an antenna to pick up all sorts of interesting hums, buzzes, noises, and RF and mainline them right into the signal path. Shielding will need to be heroic to prevent this.
There’s yet another hidden problem- because this is an iron-cored component, at low signal levels the inductance will be moving around. In transformers, this tends to be much less of an issue as long as the inductance is sufficiently large to prevent the low frequency cutoff from intermittently impinging on the audible range. But as a frequency-determining element in a filter, this is entirely unsatisfactory.
So we are left with two choices- exotic core materials and construction (read: expensive and maybe will work, kinda sorta) or some other way to supply the inductance. Being impecunious and somewhat inductor-averse, I chose the latter path and substituted a gyrator circuit.
I’m Pickin’ Up Good Gyrations
For those unfamiliar, a gyrator is a synthetic reactor (in this case, an inductor) made from active circuitry. It has the same transfer function as an ideal inductor up to a very high frequency, is stable, repeatable, and compact. In concept, it looks like this:
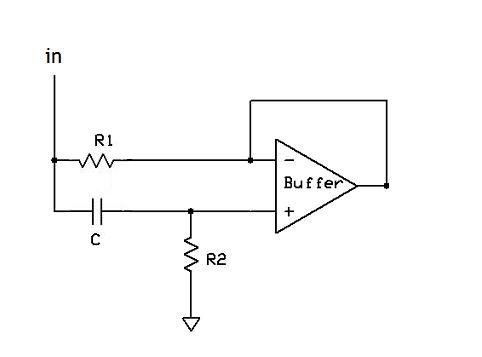
The amplifier is shown as an op-amp configured as a unity gain buffer, but can be any other sort of device with unity gain, high input impedance, and low output impedance (source follower, cathode follower…). The operation of the device is pretty simple. Generally, R2>>R1. At high frequencies, C will pass the signal to the buffer. The buffer passes that signal back to the input of the capacitor through R1. At low frequencies, the impedance of the capacitor is high, so the buffer’s input will be at ground. Thus, the impedance at “in” will be R1, a relatively low value. At high frequencies, the buffer input will be the “in” signal, which is reflected back to the buffer output; thus, both ends of R1 will be at the same potential, so no current flows through it. The only current path from the “in” is through R2, so the impedance will look like R2 (a relatively high value). At intermediate frequencies, the impedance will rise linearly since the capacitor’s impedance drops linearly with frequency. A nice cartoon simulation can be found here.
We can draw an equivalent circuit:
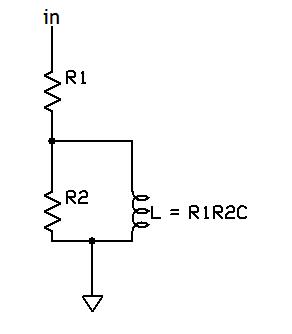
Several limitations of this circuit can be seen. First, it is only useful for circuits that have one end of the “inductor” grounded. Second, R1 is in series with the equivalent inductance, so this is only useful for circuits which require a moderately low Q (generally, less than 10). Finally, R2 sets an upper limit on the impedance- although a real inductor will trend toward infinite impedance with increasing frequency, the parallel R2 in the equivalent circuit means that the gyrator’s impedance with increasing frequency will level off at a value of R1 + R2 (which is approximately R2, since R2 >> R1).
Now, for this application, these limitations aren’t serious. We want one end of the inductor to be grounded and the required Q is quite low (0.707). And as we will demonstrate, the maximum impedance limit of R2 will occur at a frequency where it will make very little difference.
